Let’s dive into some mathematics today, in particular graph theory, to understand what triangulation is.
Definition 1.1. Let $P = \{p_1,\ldots ,p_n \} $ be a point set. A triangulation of $P$ is a maximal planar subdivision with vertex set $P$ which has $2n - 2 - k$ triangles and $3n - 3 - k$ edges where $k$ is the number of points in P on the convex hull of $ P $.
Definition 1.2. Let $P = {p_1, p_2, p_3, \ldots , p_n} $be a set of points in the Euclidian plane which are called the sites. A region of the plane obtained by assigning every point to its nearest site $p_i$ is called the _Voronoi cell_ $V(p_i)$,
$$ V(p_i) = \{ x \in \mathbb{R}^2 : d(x,p_j), \forall i \neq j \} $$
It can be interpreted as the set of all points which are closer to $p_i$ than the other sites. The set of all points that have more than one nearest neighbor is called the Voronoi diagram $\text{Vor}(P)$ for the set of sites.
Simply, the Voronoi diagram $\text{Vor}(P)$ is the subdivision of the plane into Voronoi cells $V(p)$ for all $p \in P $.
In 1934, Delaunay ( Delone, Class. Sci. Nat. (1934), 793–800.) proved that the dual graph of the Voronoi diagram drawn with straight lines produces a planar triangulation of the Voronoi sites $P$, now called the Delaunay triangulation $D(P)$.
Theorem 1.1. Let $P$ be a set of points in the plane, and let $T$ be a triangulation of $P$. Then $T$ is a Delaunay triangulation of $P$ if and only if the circumcircle of any triangle of $T$ does not contain a point of $P$ in its interior. ❑
Let’s proceed and define what edge flipping is.
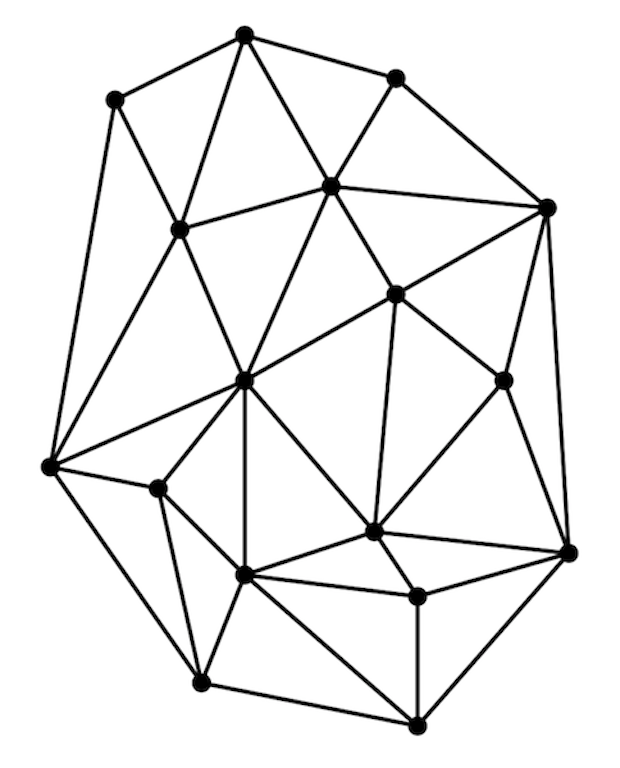
The Triangulation of a group of points.
Definition 1.3. Let $T$ be a triangulation of $P$ with $m$ triangles. Its angle vector is $A(T) = (\alpha_1, \ldots ,\alpha_{3m})$ where $\alpha_1, \ldots ,\alpha_{3m}$ are the angles of $T$ sorted by increasing value.
[ Change in angle vector, that is, $ \alpha_1,\ldots,\alpha_6 $ are replaced by $\alpha_1’ ,\ldots,\alpha_6’$ and the edge $e = \overline{p_i p_j} $ is illegal if $ min_{1 \leq i \leq 6} \alpha_i < min_{1 \leq i \leq 6} \alpha_i’$. ]
☛ We use Lemma 1 (below) to determine if an edge is illegal.
Lemma 1. The edge $ \overline{p_i p_j}$ is illegal if and only if $p_l$ lies in the interior of the circle $C$.
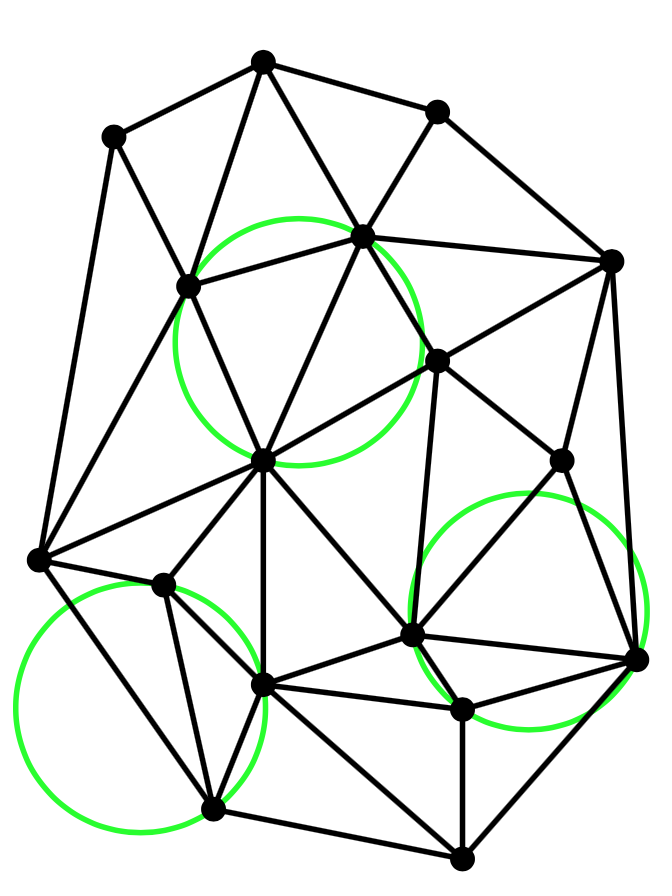
The circumcircle of any triangle of $T$ does not contain a point of $P$ in its interior.
Now finally let’s define what Delaunay Triangulation is,
Theorem 1.2. Let $P$ be a set of points in the plane, and let $T$ be a triangulation of $P$. Then $T$ is a Delaunay triangulation of $P$ if and only if the circumcircle of any triangle of $T$ does not contain a point of $P$ in its interior. ❑
This finishes the definition.
Please comment if you didn’t understand something.

